Il calcestruzzo armato 2
Nel caso di sollecitazione di taglio le travi in calcestruzzo armato evidenziano un comportamento che si discosta dalla teoria della trave di de Saint Venant e per questo motivo si richiameranno modelli differenti, senza contare che le azioni taglianti sono strettamente legate alle azioni flettenti, quindi occorre un modello che tenga conto di questo funzionamento combinato.
Come per il momento flettente si ipotizza un iniziale stato in cui permane il comportamento elastico e si inizia ad applicare la formula di Jourawski . Se la sezione si trova nello stadio I , riguardo il momento flettente, si dedurrà un diagramma τ = τ( y ) il cui valore massimo corrisponderà alla corda baricentrica e varrà 

Nel caso di corrispondenza con lo stadio II , la stessa formula di Jourawski riferita alla sezione reagente parzializzata porta a diagrammi τ = τ( y ) in cui la tensione tangenziale rimane costante in tutta la sezione parzializzata (fessurata) e pari al valore massimo sopracitato.
Questa trattazione tuttavia non tiene conto di un elemento fondamentale, e cioè che se si trascura la resistenza a trazione del calcestruzzo (ipotesi fatta nella trattazione del caso della sollecitazione flessionale) non può esserci tensione tangenziale, quindi occorre considerare il comportamento di una trave soggetta a intensità di carico via via crescenti. Fino a quando le tensioni principali di trazione non superano il limite di rottura, l'andamento delle isostatiche assume un flusso incrociato a 45° di compressioni che vanno verso il lembo superiore e di trazioni che scendono verso la mezzeria, incanalandosi orizzontalmente verso i bordi, dove si annullano le tensioni tangenziali mentre quelle normali arrivano al valore massimo.
La fessurazione si genera qualora viene raggiunto il limite di rottura della tensione principale di trazione: se avviene nella zona centrale prevalente la componente flessionale dello sforzo, la fessurazione parte dal lembo teso estendendosi in senso verticale, se avviene nei tratti terminali prevalente la componente di taglio la fessurazione compare alla quota baricentrica diretta a 45°. Nelle zone intermedie, in cui è presente sia una componente tagliante sia una componente flessionale, le fessure possono insorgere dal bordo inferiore ed estendersi con traiettoria inclinata sull'anima della trave.
Con l'insorgere della fessurazione si verifica l'ipotesi della parzializzazione che vorrebbe nella zona tesa del calcestruzzo una distribuzione costante di tensioni tangenziali. Il flusso incrociato di tensioni, di fatto, non può diffondersi uniformemente nella parte tesa della trave e quindi occorrono dei modelli più complessi per una corretta analisi della trave in fase fessurata, soprattutto vi vuole valutare la resistenza ultima al taglio (stadio III).
 | Per approfondire, vedi la voce Traliccio di Mörsch . |
Travi senza armatura a taglio
Altri contributi alla resistenza:
- Compressione assiale
- Ingranamento degli inerti ( aggregate interlock )
- Effetto Bietta ( dowel action ) è l'effetto che provocano le armature longitudinali in acciaio che attraversano le fessure nelle sezioni stesse. Tale azione contribuisce all'aumento della resistenza a sollecitazioni taglianti. La valutazione di tale contributo resistente dipende da vari fattori, quali ad esempio il diametro , la distribuzione delle barre o la granulometria degli inerti nel calcestruzzo.
L'armatura a taglio è composta da:
- Ferri piegati: ferri orizzontali piegati a 45° dall'alto verso il basso
- Staffe: ferri che possono assumere diverse forme (a U, a doppia U o rettangolari), posti perpendicolarmente rispetto ai ferri di armatura orizzontali
| Questa sezione sull'argomento ingegneria è solo un abbozzo . Contribuisci a migliorarla secondo le convenzioni di Wikipedia . |
 | Per approfondire, vedi la voce Traliccio di Rausch . |
La resistenza del conglomerato alle sollecitazioni di trazione si assume pari alla resistenza a taglio (Il valore deve essere compreso tra 0 e τc1) Se lo sforzo applicato è maggiore della resistenza del conglomerato (ma comunque minore della sua resistenza τc1) vengono utilizzate armature a spirale oppure armature orizzontali poste nelle zone soggette al massimo momento torcente (nella mezzeria della sezione)
Pilastri
 | Per approfondire, vedi la voce Pilastro . |
I pilastri sono elementi strutturali verticali atti a trasferire il carico degli impalcati alle strutture di fondazione. Sono realizzati di norma, con getti in opera anche se, in passato, sono stati realizzati con totale o parziale prefabbricazione. Con i pilastri gettati in opera è più facile realizzare un collegamento monolitico con gli altri elementi strutturali.
I pilastri sono sottoposti ai carichi verticali, orizzontali e momenti flettenti dovuti a:
• pesi propri e sovraccarichi degli impalcati trasmessi ai pilastri dalle travi di piano;
• azioni orizzontali dovuti a sisma, a vento e a dilatazioni termiche trasmesse ai pilastri dagli impalcati assunti con infinita rigidezza nel proprio piano.
Si osserva che i carichi verticali dovuti agli impalcati possono indurre elevate sollecitazioni di flessione nei pilastri per dissimetria di carico. Tale evento ricorre con frequenza nei pilastri di bordo, specie d’angolo, e tutte le volte che si verificano evidenti variazioni di luce nelle travi incidenti un pilastro. Per una sommaria valutazione del carico agente su un pilastro, si può procedere sulla base delle superfici di influenza del solaio. Per valutazioni più rigorose, si deve procedere a modelli di calcolo più appropriati come telai piani o spaziali.
Le prescrizioni poste dalla normativa per tale stato di sollecitazione sono le seguenti:
- se la sezione è poligonale l’armatura longitudinale deve prevedere almeno un ferro per ogni vertice del poligono. Se la sezione è circolare occorre prevedere almeno sei ferri longitudinali equi distribuiti;
- il diametro minimo delle armature longitudinali è di 12 mm; Per elementi prefabbricati 10 mm;
- deve essere sempre presente una armatura trasversale (staffe) di diametro maggiore od uguale a 6 mm. Le staffe devono essere chiuse e con ripiegature che entrino all’interno della sezione. Il copriferro misurato all’esterno delle staffe deve risultare maggiore od eguale a 2 cm. Le staffe debbono avere un passo non maggiore a quindici volte il diametro minimo delle armature longitudinali e comunque non superiore a 25 cm.
- L’armatura longitudinale deve:
- risultare maggiore od uguale all’otto per mille della sezione di conglomerato strettamente necessaria;
- risultare maggiore del tre per mille della sezione effettiva di conglomerato;
- risultare minore del sei per cento della sezione effettiva di conglomerato.
Tale sollecitazione può essere sia di compressione che di trazione e generalmente incide su elementi strutturali come i pilastri.
 | Per approfondire, vedi la voce Pilastro . |
Tali elementi in cemento armato sono provvisti di due ordini di armature, una longitudinale costituita da ferri posti generalmente agli spigoli della sezione (ed eventualmente anche sui lati più lunghi della medesima) ed una trasversale costituita da ferri, sagomati similmente alla sezione in modo da racchiudere il fascio di ferri longitudinali, detti staffe .
Nei pilastri sottoposti all'azione di compressione non sorgono generalmente tensioni di trazione , si potrebbe dunque non adottare alcuna armatura metallica in virtù della resistenza a compressione del calcestruzzo. Tuttavia la fragilità del calcestruzzo richiede un correttivo e si tende ad adottare una "gabbia" metallica superficiale. Tale gabbia va rapportata alla massa di conglomerato da armare, in modo da ottenere una prescrizione sulle armature minime secondo la relazione:

in cui si impone il valore minimo ρ 0 (per esempio  ) al rapporto geometrico d'armatura longitudinale ρ s , quindi
) al rapporto geometrico d'armatura longitudinale ρ s , quindi
 Calcolo elastico
Calcolo elastico Data una sezione in calcestruzzo armato soggetta ad una forza N centrata di compressione, la prima ipotesi di calcolo si pone che la sezione stessa trasli rimanendo piana, manifestando sotto carico una deformazione ε costante (in questo caso una contrazione), che vi sia perfetta aderenza tra i due materiali, derivandone che entrambi subiscono la stessa deformazione ( ε s = ε c = ε ) e che non la sezione reagente al carico coincida con la sezione geometrica.
Per un calcolo elastico, le tensioni nei due materiali si ottengono attraverso la legge di Hooke :
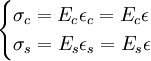
In virtù dell'ipotesi di eguaglianza tra le deformazioni si ha che σ s = m σ c con m = E s / E c . L'equilibrio alla traslazione della sezione si pone con la seguente relazione

A i è definita l'area ideale della sezione ragguagliata al calcestruzzo, ovvero si "trasforma", attraverso un coefficiente di omogenizzazione m , l'area dell'acciaio in area di calcestruzzo. Definendo rapporto elastico d'armatura

si può scrivere che:

Il valore delle tensioni generate dallo sforzo normale centrato N valgono

Assumendo il valore caratteristico dell'azione, tali formule si impiegano per le verifiche di esercizio  con
con  per situazioni non transitorie di carico.
per situazioni non transitorie di carico.
Calcolo a rottura
Per il calcolo a rottura o allo stato limite ultimo l'ipotesi elastica va sostituita con le leggi costitutive σ − ε dei due materiali.
Nelle sezioni di calcestruzzo compresse assialmente non si hanno, a differenza delle travi inflesse in cui la variabilità delle tensioni offre un certo grado di "iperstaticità" al sistema, situazioni in cui vi siano fibre della sezione meno caricate che offrono il controllo alle deformazioni rispetto a quelle più caricate.
Per tale motivo si assume il limite ε c 1 quale contrazione limite di rottura. La presenza di armatura, qualora non sia già snervata, potrebbe fornire un ulteriore controllo delle deformazioni per poter superare tale valore, almeno fino al limite di snervamento della stessa armatura, raggiunto il quale si perde ogni iperstaticità interna.
Supposto quindi un incremento istantaneo di carico, l'equilibrio della sezione si pone con l'equazione:

dove σ * = f s d qualora risulti che ε y d < ε c 1 . In modo analogo alla formula elastica si ottiene
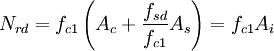
dove l'area ideale ragguagliata al calcestruzzo vale

In questo caso il coefficiente di omogenizzazione dell'area metallica è dato dal rapporto delle due tensioni resistenti, mentre il coefficiente adimensionale, detto rapporto meccanico d'armatura indica l'apporto relativo dell'armatura metallica in confronto alla resistenza secondo la relazione
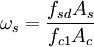
Per capire l'ordine di grandezza del rapporto meccanico d'armatura si valutano tre situzioni:
| Inferiore | Tipo minore d'acciaio con classe maggiore di cls |  |
| Intermedio | Accoppiamento più equilibrato di materiali |  |
| Superiore | Tipo maggiore d'acciaio con classe minore di cls |  |
Secondo la normativa italiana la relazione d'equilibrio per il calcolo della sezione diventa
 Sforzo normale eccentrico
Sforzo normale eccentrico | Questa sezione è ancora vuota . Aiutaci a scriverla! |
Altri elementi costruttivi in calcestruzzo armato [ modifica ]
 | Per approfondire, vedi le voci Fondazione (architettura) e Muro di sostegno . |
| Questa sezione è ancora vuota . Aiutaci a scriverla! |
Bibliografia
- Giandomenico Toniolo, Cemento armato - Calcolo agli stati limite vol. 2A-2B , Zanichelli, 1993.